Research

Navier-Stokes equations and turbulence

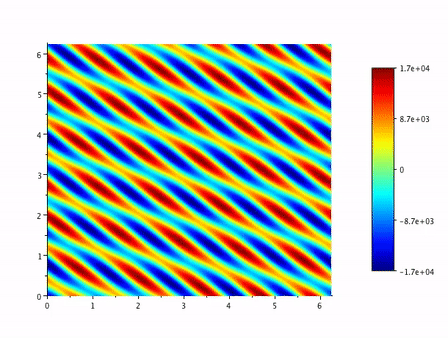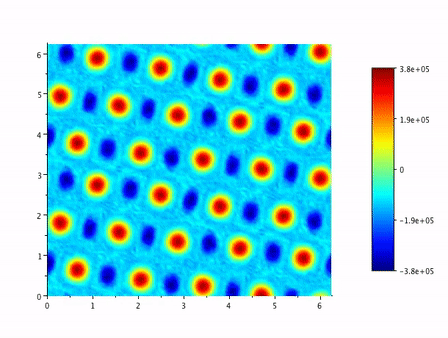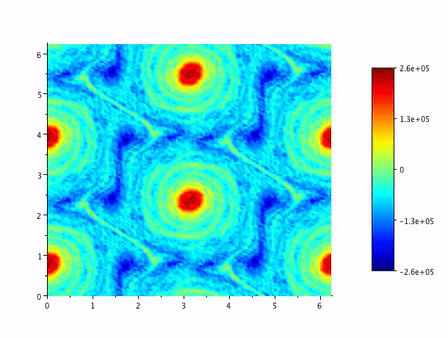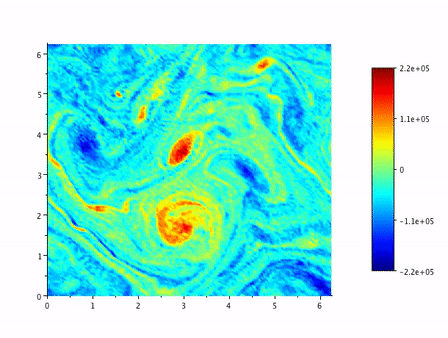
Level sets of vorticity in a periodic, two-mode-forced incompressible 2D Navier-Stokes pseudo-spectrally simulated flow. (Click here for an extended simulation))

Turbulence is a fascinating phenomenom. It occurs in many types of fluids under various conditions. From the most visible ones, as in the formation of currents in rivers, to more hidden ones, as the flow of blood and other fluids in our bodies, of oil and gas in pipelines and wellbores, and of magma in the Earth's mantle and in magma chambers.

Despite the fact that there are well-accepted mathematical models to describe the motion of the associated fluid flows, explicit solutions to the modeling systems of equations exist only in very particular cases, so that alternative routes are needed.

Numerical solutions are largely exploited in engineering problems. However, in the case of turbulent flows, the complexity of the flow is such that the required mesh resolution for numerically modelling the dynamics of all the energetic spatial and temporal structures of the flow is impracticle for the current and even forthcoming computational power. Hence, appropriate simplifications and lower dimensional models must still be used. For this reason, research in turbulence is still a very active field.

My research mainly focuses on the system of equations known as the homogeneous and incompressible Navier-Stokes equations (iNSE), which is a model for the flow of certain Newtonian fluids such as water and oil, under most conditions. In a sense, this is the simplest possible type of fluid, but which already presents many theoretical and practical challenges.

In particular, the question of well-posedness of the iNSE is still an open problem and is currently a point of intense research due to some recent advances in similar problems. This question is one of the Millenium Problems, for which there is a one-million dolar prize.

My interest, however, is mostly devoted to building a mathematical foundation for rigorous results related to turbulence. This comprises

looking for estimates of turbulence-related time-averaged mean quantities for Leray-Hopf weak solutions of the iNSE; developing and analysing a proper framework for statistical solutions of the iNSE as a rigorous way of assessing ensemble averages of the flow; and numerically investigating the results associated with the previous two items.

Abstract statistical solutions

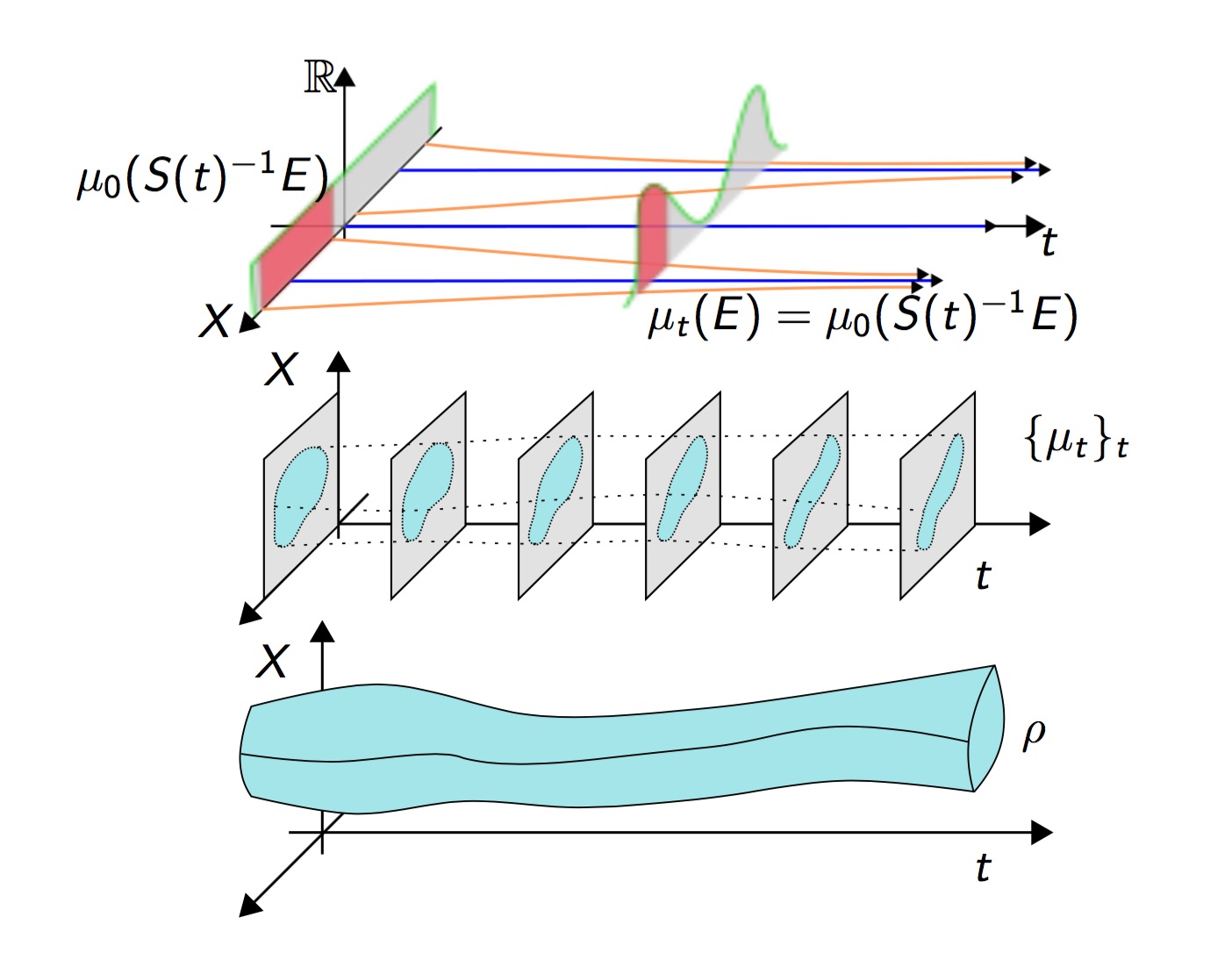
Representation of a push-forward of an initial measure by a semigroup (top); a phase-space statistical solution (middle); and a trajectory statistical solution (bottom).

This work stemmed from the study of statistical solutions of the Navier-Stokes. It aims towards a generalization of this notion to various types of evolution equations.

An abstract framework is formulated in which the phase-space of the evolutionary system is assumed to be a Hausdorff topological space, and the evolution equation is considered in a weak sense, in the dual of a topological vector space.

The main results obtained so far in this context are

1. the existence of solutions to the associated initial value problem under simple and natural conditions;

2. a vast number of applications showing the applicability of the theory; and

3. conditions for the convergence of subnets of statistical solutions depending on parameters of a family of equations.

There are challenging functional-analytic and measure-theoretic problems involved in this line of research due to the high degree of abstraction and the need to be as applicable as possible.

Infinite-dimensional dynamical systems

The "Dynamic Sugar Loaf", made of a heteroclinic cycle, a repeller focus as the Sun, and water waves completing the picture of a famous landmark in Rio de Janeiro.

Several real-life phenomena and advanced technological problems are modeled with systems involving evolutionary partial differential equations. Such systems appear in a multitude of areas, such as Physics, Engineering, Biology, Chemistry, Biochemistry, Finance, and so on.

As evolutionary partial differential equations, they may generate dynamical systems in phase spaces which are of infinite dimension. Many of these systems have very rich dynamics.

The study of evolutionary partial differential equations is thus of great interest and very challenging.

I started my research precisely in this area, working on it since my MSc at IM-UFRJ, continuing on it during my PhD at the Indiana University and thereafter. The study of evolutionary nonlinear partial differential equations as infinite-dimensional dynamical system was just taking off prior to my MSc and have been flourishing since then.

I have worked on several different types of nonlinear partial differential equations, from reaction-diffusion equations, to fluid-flow, dispersive, and wave-type equations. Currently, I have been working on fluid-flow models with viscous heating, important in some situations of magma flows and certain oil flows in pipelines.

Important questions in this field include

1. assessing the local well posedness of the system;

2. assessing the global well-posedness of the system and the existence of an associated dynamical system;

3. understanding the complexity of the associated dynamics;

4. analysing the possible finite-dimensionality of the asymptotic behavior of the system;

5. looking for finite-dimensional systems mimicking or approximating the dynamics of the system;

6. understanding the effect of the approximation of the infinite-dimensional system by finite-dimensional numerical schemes;

7. exploiting the finite dimensional asymptotic behavior of some system for control purposes; and so on.

Modeling the salt and pre-salt layers for pre-salt oil exploitation

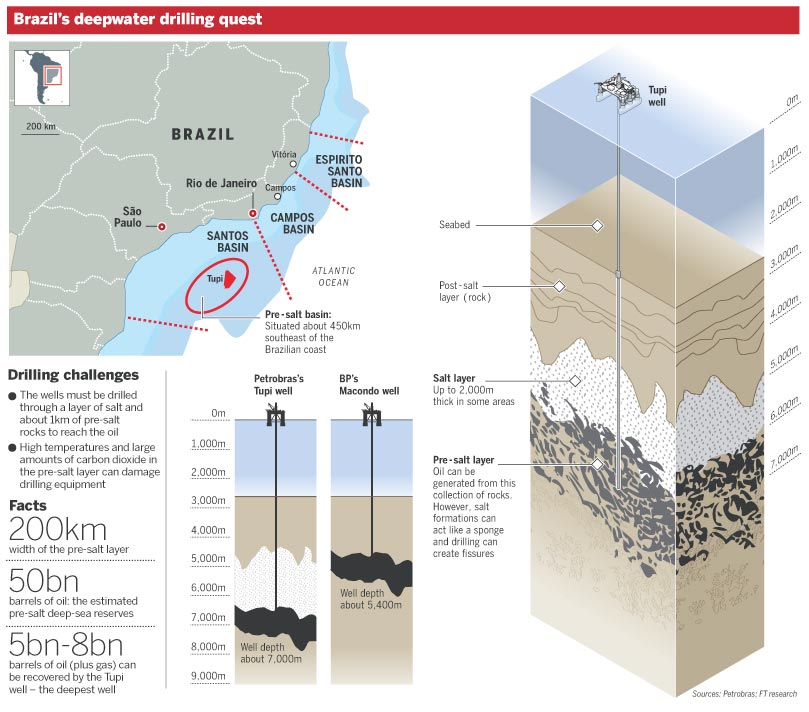
Deep water prospection aspects

The salt layer, below, in yellow, modeled as a visco-elastic fluid, and being deformed into "mushroom"-like diapirs (geological intrusion), under the load of different layers of elastic sedimentary rocks.

Pre-salt oil became a fundamental asset for Brazil, but its exploitation is an extraordinary task.

The oil prospected before the pre-salt era lies in sedimentary layers at the bottom of the ocean or below ground. The pre-salt oil, on the other hand, lies within a carbonaceous layer, just below a thick 2km salt layer, which is below the sedimentary layers, and at the bottom of the ocean. The difficulties for prospection are enormous.

The aim of this project was initially to find a better model for the kinematics of the salt layer and then to study the behavior of the salt layer according to this model.

Salt rocks in the Earth's crust behave as solids on small time scales, but display a viscoelastic behavior on intermediate and long time scales. Some works assume a Newtonian viscous model or an Oldroyd-B visco-elastic model. We consider, on the other hand, a more general visco-elastic model proposed by I-Shi Liu (IM-UFRJ) that we termed the Mooney-Rivlin-Liu model.

Using experimental data obtained from a number of tests on samples of different types of salt rocks, we have showed that our model fits considerably better the observed deformations.

Having validated the model, we studied its analytical properties as well as some qualitive properties relevant for

1. the evolution of the salt layer in the Earth's crust;

2. the formation of salt diapirs flowing into the upper sediment layer;

3. the mechanical properties involved in the drilling process of boreholes through the salt layer; and

4. the optimization of the drilling path throught the different layers.

This is a joint project with CENPES/PETROBRÁS. We are now renewing this project to continue researching the properties of the salt layer and to include developing a model for the pre-salt layer and analysing the interaction between all those layers according to these models.

These diverse studies involve analysis of partial differential equations, dynamical systems, optimization methods, numerical analysis, and computer simulations.

Mathematics in the brewing process

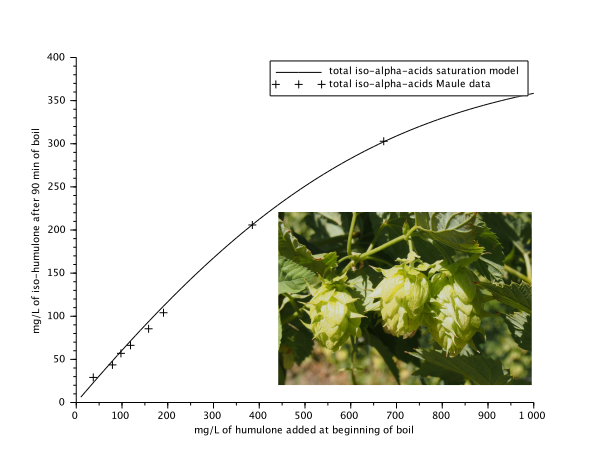
Hop flowers and a plot of an experimental data of the humulone to iso-humulone conversion and a fitting by a saturation model.

There is a multitude of physical, chemical, and biological processes ocurring during the brewing and storage stages of beer manufacture.

Many of these processes can be given a mathematical formulation, and most of them can be modeled with systems of ordinary or partial differential equations. These are the sort of models that interest me the most (besides drinking the end product, of course).

From the physicochemical processes that turn the starch within the barley malt (one of the four main ingredients of beer) into the sugary wort that feeds the yeast (the most fundamental ingredient of beer); to the physicochemical process that turn the bitter and slightly soluble alpha-acids present in the hops (the third main ingredient of beer in this list) into the much more bitter and more soluble iso-alpha-acids that help balance the lingering sweetness that remains from the wort; to the biochemical processes involved when the yeast turns most of the sugar in the wort into alchohol and other aromatic compounds that make for a delicious (or not) beer. These are typical processes where ordinary differential equations can be used as models. (In case you notice anything missing, the fourth ingredient not mentioned yet is the most abundant one, namely water, which serves as the solvent for the other compounds.)

In most situations these processes can be assumed to occur within a spatially homogeneous and static medium, leading to systems of ordinary differential equations. Sometimes, however, the proccess requires the media to be treated as a flowing fluid, either as Newtonian-type flow inside a mash tun, a kettle, or a fermentation tank, or as a fluid flowing through a porous bed of spent grains, as in the sparging step. These processes lead to partial differential equations and are particularly important in the very design of the equipment, for efficiency (optimization) purposes.